The New York Times recently introduced a new daily puzzle called Pips. The idea is to place a set of dominoes on a grid, satisfying various conditions. For instance, in the puzzle below, the four dominoes must be positioned to satisfy three conditions: the pips (dots) in the purple squares must sum to 8, there must be fewer than 5 pips in the red square, and the pips in the three green squares must be equal. (It doesn't take much thought to solve this "easy" puzzle, but the "medium" and "hard" puzzles are more challenging.)
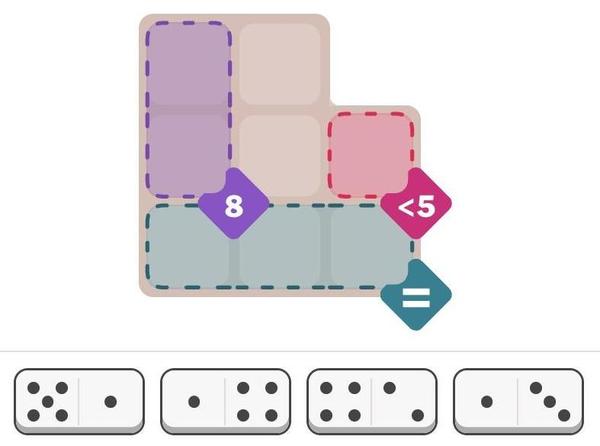
I was wondering about how to solve these puzzles with a computer. Recently, I saw an article on Hacker News—"Many hard LeetCode problems are easy constraint problems"—that described the benefits and flexibility of a system called a constraint solver. A constraint solver takes a set of constraints and finds solutions that satisfy the constraints: exactly what Pips requires.
I figured that solving Pips with a constraint solver would be a good way to learn more about these solvers, but I had several questions. Did constraint solvers require incomprehensible mathematics? How hard was it to express a problem? Would the solver quickly solve the problem, or would it get caught in an exponential search?
It turns out that using a constraint solver was straightforward; it took me under two hours from knowing nothing about constraint solvers to solving the problem. The solver found solutions in milliseconds (for the most part). However, there were a few bumps along the way. In this blog post, I'll discuss my experience with the MiniZinc1 constraint modeling system and show how it can solve Pips.
Approaching the problem
Writing a program for a constraint solver is very different from writing a regular program. Instead of telling the computer how to solve the problem, you tell it what you want: the conditions that must be satisfied. The solver then "magically" finds solutions that satisfy the problem.
To solve the problem, I created an array called pips that holds the number of domino pips at each position in the grid. Then, the three constraints for the above problem can be expressed as follows. You can see how the constraints directly express the conditions in the puzzle.
constraint pips[1,1] + pips[2,1] == 8; constraint pips[2,3]Next, I needed to specify where dominoes could be placed for the puzzle. To do this, I defined an array called grid that indicated the allowable positions: 1 indicates a valid position and 0 indicates an invalid position. (If you compare with the puzzle at the top of the article, you can see that the grid below matches its shape.)
grid = [| 1,1,0| 1,1,1| 1,1,1|];I also defined the set of dominoes for the problem above, specifying the number of spots in each half:
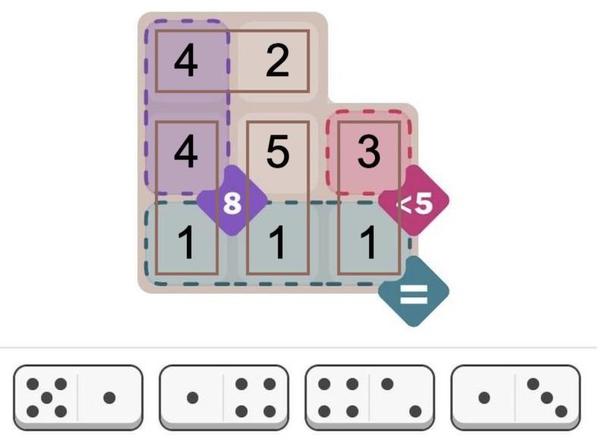
spots = [|5,1| 1,4| 4,2| 1,3|];So far, the constraints directly match the problem. However, I needed to write some more code to specify how these pieces interact. But before I describe that code, I'll show a solution. I wasn't sure what to expect: would the constraint solver give me a solution or would it spin forever? It turned out to find the unique solution in 109 milliseconds, printing out the solution arrays. The pips array shows the number of pips in each position, while the dominogrid array shows which domino (1 through 4) is in each position.
pips = [| 4, 2, 0 | 4, 5, 3 | 1, 1, 1 |]; dominogrid = [| 3, 3, 0 | 2, 1, 4 | 2, 1, 4 |];The text-based solution above is a bit ugly. But it is easy to create graphical output. MiniZinc provides a JavaScript API, so you can easily display solutions on a web page. I wrote a few lines of JavaScript to draw the solution, as shown below. (I just display the numbers since I was too lazy to draw the dots.) Solving this puzzle is not too impressive—it's an "easy" puzzle after all—but I'll show below that the solver can also handle considerably more difficult puzzles.
Details of the code
While the above code specifies a particular puzzle, a bit more code is required to define how dominoes and the grid interact. This code may appear strange because it is implemented as constraints, rather than the procedural operations in a normal program.
My main design decision was how to specify the locations of dominoes. I considered assigning a grid position and orientation to each domino, but it seemed inconvenient to deal with multiple orientations. Instead, I decided to position each half of the domino independently, with an x and y coordinate in the grid.2 I added a constraint that the two halves of each domino had to be in neighboring cells, that is, either the X or Y coordinates had to differ by 1.
constraint forall(i in DOMINO) (abs(x[i, 1] - x[i, 2]) + abs(y[i, 1] - y[i, 2]) == 1);It took a bit of thought to fill in the pips array with the number of spots on each domino. In a normal programming language, one would loop over the dominoes and store the values into pips. However, here it is done with a constraint so the solver makes sure the values are assigned. Specifically, for each half-domino, the pips array entry at the domino's x/y coordinate must equal the corresponding spots on the domino:
constraint forall(i in DOMINO, j in HALF) (pips[y[i,j], x[i, j]] == spots[i, j]);I decided to add another array to keep track of which domino is in which position. This array is useful to see the domino locations in the output, but it also keeps dominoes from overlapping. I used a constraint to put each domino's number (1, 2, 3, etc.) into the occupied position of dominogrid:
constraint forall(i in DOMINO, j in HALF) (dominogrid[y[i,j], x[i, j]] == i);Next, how do we make sure that dominoes only go into positions allowed by grid? I used a constraint that a square in dominogrid must be empty or the corresponding grid must allow a domino.3 This uses the "or" condition, which is expressed as \/, an unusual stylistic choice. (Likewise, "and" is expressed as /\. These correspond to the logical symbols ∨ and ∧.)
constraint forall(i in 1..H, j in 1..W) (dominogrid[i, j] == 0 \/ grid[i, j] != 0);Honestly, I was worried that I had too many arrays and the solver would end up in a rathole ensuring that the arrays were consistent. But I figured I'd try this brute-force approach and see if it worked. It turns out that it worked for the most part, so I didn't need to do anything more clever.
Finally, the program requires a few lines to define some constants and variables. The constants below define the number of dominoes and the size of the grid for a particular problem:
int: NDOMINO = 4; % Number of dominoes in the puzzle int: W = 3; % Width of the grid in this puzzle int: H = 3; % Height of the grid in this puzzleNext, datatypes are defined to specify the allowable values. This is very important for the solver; it is a "finite domain" solver, so limiting the size of the domains reduces the size of the problem. For this problem, the values are integers in a particular range, called a set:
set of int: DOMINO = 1..NDOMINO; % Dominoes are numbered 1 to NDOMINO set of int: HALF = 1..2; % The domino half is 1 or 2 set of int: xcoord = 1..W; % Coordinate into the grid set of int: ycoord = 1..H;At last, I define the sizes and types of the various arrays that I use. One very important syntax is var, which indicates variables that the solver must determine. Note that the first two arrays, grid and spots do not have var since they are constant, initialized to specify the problem.
array[1..H,1..W] of 0..1: grid; % The grid defining where dominoes can go array[DOMINO, HALF] of int: spots; % The number of spots on each half of each domino array[DOMINO, HALF] of var xcoord: x; % X coordinate of each domino half array[DOMINO, HALF] of var ycoord: y; % Y coordinate of each domino half array[1..H,1..W] of var 0..6: pips; % The number of pips (0 to 6) at each location. array[1..H,1..W] of var 0..NDOMINO: dominogrid; % The domino sequence number at each locationYou can find all the code on GitHub. One weird thing is that because the code is not procedural, the lines can be in any order. You can use arrays or constants before you use them. You can even move include statements to the end of the file if you want!
Complications
Overall, the solver was much easier to use than I expected. However, there were a few complications.
By changing a setting, the solver can find multiple solutions instead of stopping after the first. However, when I tried this, the solver generated thousands of meaningless solutions. A closer look showed that the problem was that the solver was putting arbitrary numbers into the "empty" cells, creating valid but pointlessly different solutions. It turns out that I didn't explicitly forbid this, so the sneaky constraint solver went ahead and generated tons of solutions that I didn't want. Adding another constraint fixed the problem. The moral is that even if you think your constraints are clear, solvers are very good at finding unwanted solutions that technically satisfy the constraints. 4
A second problem is that if you do something wrong, the solver simply says that the problem is unsatisfiable. Maybe there's a clever way of debugging, but I ended up removing constraints until the problem can be satisfied, and then see what I did wrong with that constraint. (For instance, I got the array indices backward at one point, making the problem insoluble.)
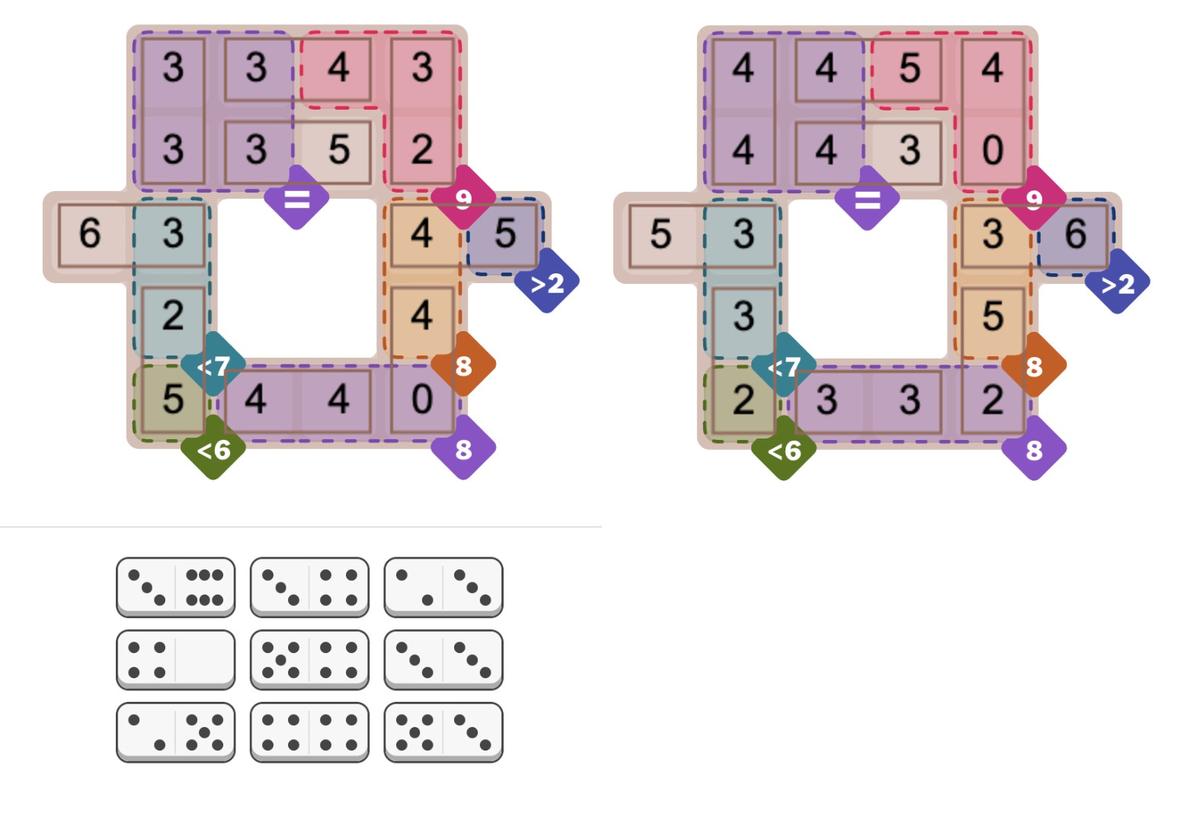
The most concerning issue is the unpredictability of the solver: maybe it will take milliseconds or maybe it will take hours. For instance, the Oct 5 hard Pips puzzle (below) caused the solver to take minutes for no apparent reason. However, the MiniZinc IDE supports different solver backends. I switched from the default Gecode solver to Chuffed, and it immediately found numerous solutions, 384 to be precise. (Sometimes the Pips puzzles sometimes have multiple solutions, which players find controversial.) I suspect that the multiple solutions messed up the Gecode solver somehow, perhaps because it couldn't narrow down a "good" branch in the search tree. For a benchmark of the different solvers, see the footnote.5
How does a constraint solver work?
If you were writing a program to solve Pips from scratch, you'd probably have a loop to try assigning dominoes to positions. The problem is that the problem grows exponentially. If you have 16 dominoes, there are 16 choices for the first domino, 15 choices for the second, and so forth, so about 16! combinations in total, and that's ignoring orientations. You can think of this as a search tree: at the first step, you have 16 branches. For the next step, each branch has 15 sub-branches. Each sub-branch has 14 sub-sub-branches, and so forth.
An easy optimization is to check the constraints after each domino is added. For instance, as soon as the "less than 5" constraint is violated, you can backtrack and skip that entire section of the tree. In this way, only a subset of the tree needs to be searched; the number of branches will be large, but hopefully manageable.
A constraint solver works similarly, but in a more abstract way. The constraint solver assigns values to the variables, backtracking when a conflict is detected. Since the underlying problem is typically NP-complete, the solver uses heuristics to attempt to improve performance. For instance, variables can be assigned in different orders. The solver attempts to generate conflicts as soon as possible so large pieces of the search tree can be pruned sooner rather than later. (In the domino case, this corresponds to placing dominoes in places with the tightest constraints, rather than scattering them around the puzzle in "easy" spots.)
Another technique is constraint propagation. The idea is that you can derive new constraints and catch conflicts earlier. For instance, suppose you have a problem with the constraints "a equals c" and "b equals c". If you assign "a=1" and "b=2", you won't find a conflict until later, when you try to find a value for "c". But with constraint propagation, you can derive a new constraint "a equals b", and the problem will turn up immediately. (Solvers handle more complicated constraint propagation, such as inequalities.) The tradeoff is that generating new constraints takes time and makes the problem larger, so constraint propagation can make the solver slower. Thus, heuristics are used to decide when to apply constraint propagation.
Researchers are actively developing new algorithms, heuristics, and optimizations6 such as backtracking more aggressively (called "backjumping"), keeping track of failing variable assignments (called "nogoods"), and leveraging Boolean SAT (satisfiability) solvers. Solvers compete in annual challenges to test these techniques against each other. The nice thing about a constraint solver is that you don't need to know anything about these techniques; they are applied automatically.
Conclusions
I hope this has convinced you that constraint solvers are interesting, not too scary, and can solve real problems with little effort. Even as a beginner, I was able to get started with MiniZinc quickly. (I read half the tutorial and then jumped into programming.)
One reason to look at constraint solvers is that they are a completely different programming paradigm. Using a constraint solver is like programming on a higher level, not worrying about how the problem gets solved or what algorithm gets used. Moreover, analyzing a problem in terms of constraints is a different way of thinking about algorithms. Some of the time it's frustrating when you can't use familiar constructs such as loops and assignments, but it expands your horizons.
Finally, writing code to solve Pips is more fun than solving the problems by hand, at least in my opinion, so give it a try!
For more, follow me on Bluesky (@righto.com), Mastodon (@kenshirriff@oldbytes.space), RSS, or subscribe here.
Notes and references
-
There are several different constraint solvers available. I arbitrarily chose MiniZinc, since it was described in the article I read, but Google's XXX is another approach. I started by downloading the MiniZinc IDE and reading the MiniZinc tutorial. After reading half the tutorial, I decided to jump in and see if I could make it work.
The MiniZinc IDE is straightforward, with an editor window at the top and an output window at the bottom. Clicking the "Run" button causes it to generate a solution.
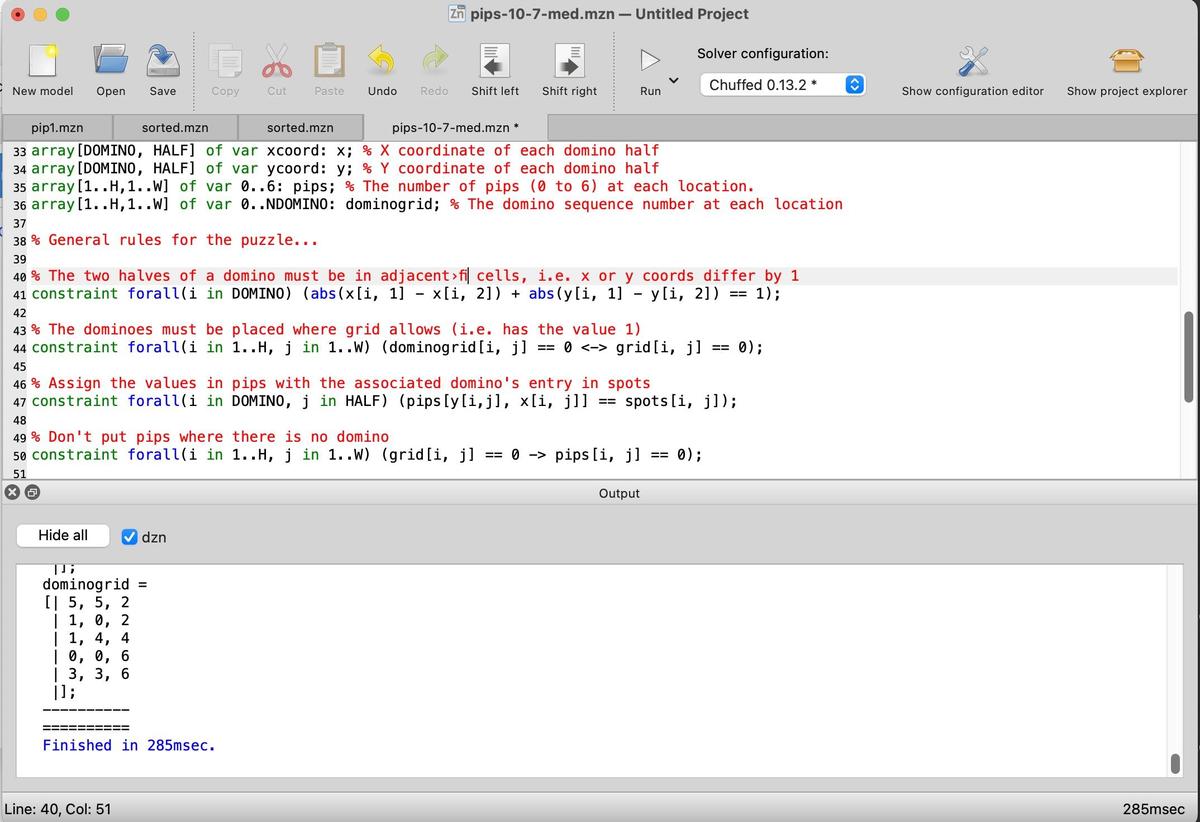 Screenshot of the MiniZinc IDE. Click for a larger view.
Screenshot of the MiniZinc IDE. Click for a larger view.↩
-
It might be cleaner to combine the X and Y coordinates into a single Point type, using a MiniZinc record type. ↩
-
I later decided that it made more sense to enforce that dominogrid is empty if and only if grid is 0 at that point, although it doesn't affect the solution. This constraint uses the "if and only if" operator <->.
constraint forall(i in 1..H, j in 1..W) (dominogrid[i, j] == 0 <-> grid[i, j] == 0); ↩ -
To prevent the solver from putting arbitrary numbers in the unused positions of pips, I added a constraint to force these values to be zero:
constraint forall(i in 1..H, j in 1..W) (grid[i, j] == 0 -> pips[i, j] == 0);Generating multiple solutions had a second issue, which I expected: A symmetric domino can be placed in two redundant ways. For instance, a double-six domino can be flipped to produce a solution that is technically different but looks the same. I fixed this by adding constraints for each symmetric domino to allow only one of the two redundant positions. The constraint below forces a preferred orientation for symmetric dominoes.
constraint forall(i in DOMINO) (spots[i,1] != spots[i,2] \/ x[i,1] > x[i,2] \/ (x[i,1] == x[i,2] /\ y[i,1] > y[i,2]));To enable multiple solutions in MiniZinc, the setting is under Show Configuration Editor > User Defined Behavior > Satisfaction Problems or the --all flag from the command line. ↩
-
MiniZinc has five solvers that can solve this sort of integer problem: Chuffed, OR Tools CP-SAT, Gecode, HiGHS, and Coin-OR BC. I measured the performance of the five solvers against 20 different Pips puzzles. Most of the solvers found solutions in under a second, most of the time, but there is a lot of variation.
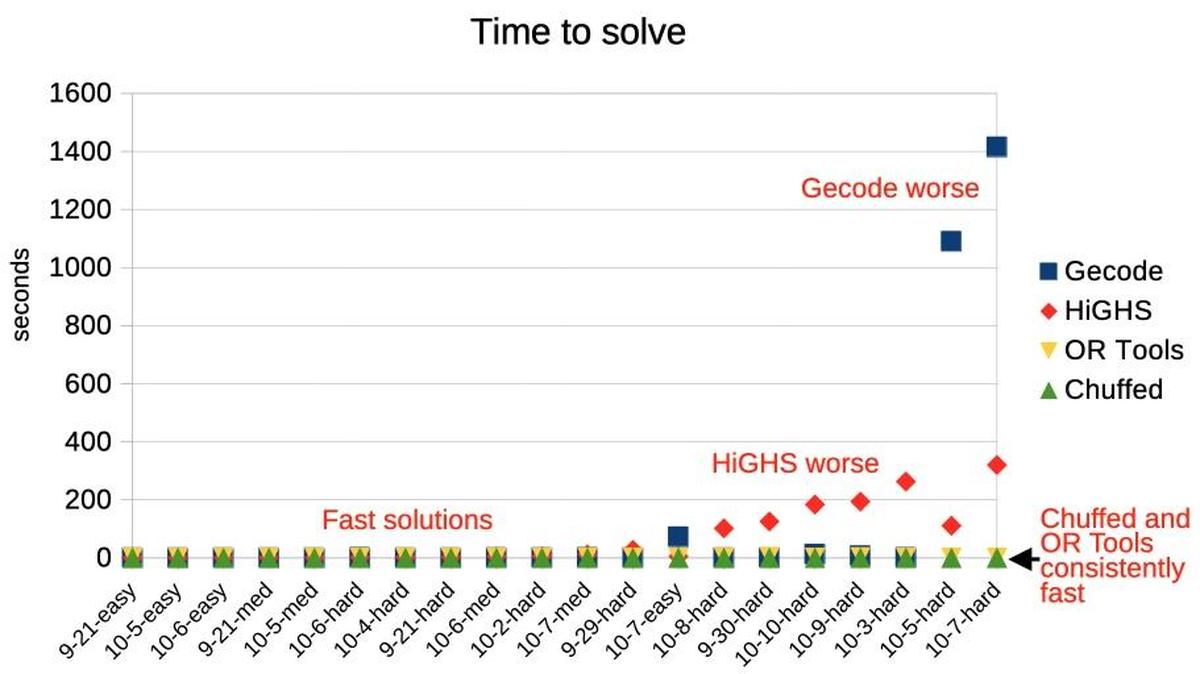 Timings for different solvers on 20 Pip puzzles.
Timings for different solvers on 20 Pip puzzles.Overall, Chuffed had the best performance on the puzzles that I tested, taking well under a second. Google's OR-Tools won all the categories in the 2025 MiniZinc challenge, but it was considerably slower than Chuffed for my Pips programs. The default Gecode solver performed very well most of the time, but it did terribly on a few problems, taking over 15 minutes. HiGHs was slower in general, taking a few minutes on the hardest problems, but it didn't fail as badly as Gecode. (Curiously, Gecode and HiGHS sometimes found different problems to be difficult.) Finally, Coin-OR BC was uniformly bad; at best it took a few seconds, but one puzzle took almost two hours and others weren't solved before I gave up after two hours. (I left Coin-OR BC off the graph because it messed up the scale.)
Don't treat these results too seriously because different solvers are optimized for different purposes. (In particular, Coin-OR BC is designed for linear problems.) But the results demonstrate the unpredictability of solvers: maybe you get a solution in a second and maybe you get a solution in hours. ↩
-
If you want to read more about solvers, Constraint Satisfaction Problems is an overview presentation. The Gecode algorithms are described in a nice technical report: Constraint Programming Algorithms used in Gecode. Chuffed is more complicated: "Chuffed is a state of the art lazy clause solver designed from the ground up with lazy clause generation in mind. Lazy clause generation is a hybrid approach to constraint solving that combines features of finite domain propagation and Boolean satisfiability." The Chuffed paper Lazy clause generation reengineered and slides are more of a challenge. lecture slides. --> ↩























 24h Most Popular
24h Most Popular






 Utilities
Utilities